Lección 2

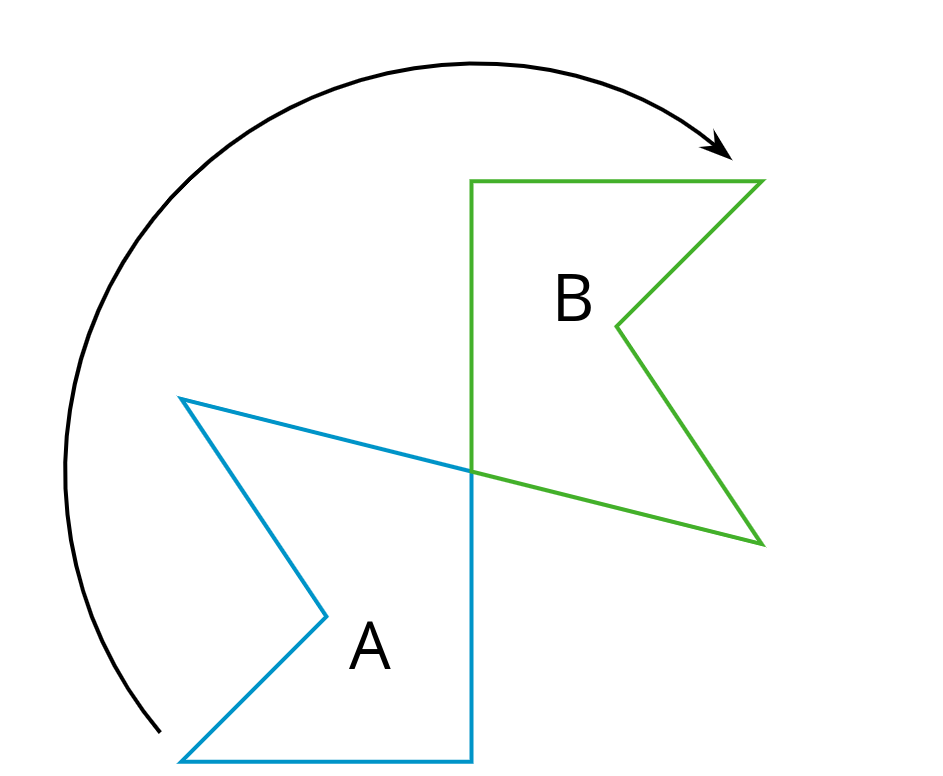
El cuadrilátero A se puede rotar a la posición del cuadrilátero B.

Estima el ángulo de rotación.

Este es un nuevo conjunto de pasos de baile.

1. Describan cada movida o digan si es una nueva movida.

   1. Recuadro 1 a recuadro 2.

   2. Recuadro 2 a recuadro 3.

   3. Recuadro 3 a recuadro 4.

   4. Recuadro 4 a recuadro 5.

   5. Recuadro 5 a recuadro 6.

2. ¿Cómo describirían la nueva movida?

Su profesor les dará un juego de tarjetas. Clasifiquen las tarjetas en categorías según el tipo de movida que muestran. Prepárense para describir cada categoría y explicar por qué es diferente de las demás.

Estas son las movidas que hemos aprendido hasta ahora:

• Una traslación desliza una figura sin girarla. Cada punto de la figura recorre la misma distancia en la misma dirección. Por ejemplo, la figura A se trasladó hacia abajo y hacia la izquierda, como se muestra con las flechas. La figura B es una traslación de la figura A.

  

  

• Una rotación gira una figura alrededor de un punto, llamado el centro de rotación. Cada punto de la figura va en un círculo alrededor del centro y gira el mismo ángulo. La rotación puede ser en el sentido de las manecillas del reloj o en el sentido contrario a las manecillas del reloj. Por ejemplo, la figura A se rotó \(45^\circ\) en el sentido de las manecillas del reloj alrededor de su vértice inferior. La figura C es una rotación de la figura A.

  

  

• Una reflexión ubica los puntos en el lado opuesto de una recta de reflexión. La imagen espejo es una copia al revés de la figura original. La recta de reflexión muestra dónde se debería ubicar el espejo. Por ejemplo, la figura A se reflejó sobre la recta punteada. La figura D es una reflexión de la figura A.

  

  

Usamos la palabra imagen para describir una nueva figura que se creó moviendo la figura original. Si un punto de la figura original se mueve a un punto de la nueva figura, los llamamos puntos correspondientes.