Lección 4
Razonemos sobre ecuaciones y diagramas de cinta (Parte 1)
Observemos cómo los diagramas de cinta pueden ayudarnos a responder preguntas sobre cantidades desconocidas en unas historias.
Problema 1
Dibuja un cuadrado con lado de longitud 7 cm.
- Predice el perímetro y la longitud de la diagonal del cuadrado.
- Mide el perímetro y la longitud de la diagonal del cuadrado.
- Describe qué tan parecidas son las predicciones y las mediciones.
Problema 2
Halla los productos.
- \((100) \boldcdot (\text-0.09)\)
- \((\text-7) \boldcdot (\text- 1.1)\)
- \((\text-7.3) \boldcdot (5)\)
- \((\text-0.2) \boldcdot (\text-0.3)\)
Problema 3
Estas son tres historías:
-
Una familia compra 6 boletos para un espectáculo y además pagan \$3 por el estacionamiento. Gastan \$27 para ver el espectáculo.
-
Diego tiene 27 onzas de jugo. Le sirve cantidades iguales de jugo a cada uno de sus 3 amigos y quedan 6 onzas para él.
-
Jada trabaja 6 horas preparándose para la feria de arte. Gasta 3 horas en una escultura y luego pinta 27 cuadros.
Estas son tres ecuaciones:
- \(3x+6=27\)
- \(6x+3=27\)
- \(27x+3=6\)
- Decide cuál ecuación representa cada historia. ¿Qué representa \(x\) en cada ecuación?
- Encuentra la solución para cada ecuación. Explica o muestra tu razonamiento.
- ¿Qué te dice cada solución acerca de la situación?
Problema 4
Este es un diagrama junto con su ecuación correspondiente. Encuentra la solución a la ecuación y explica tu razonamiento.
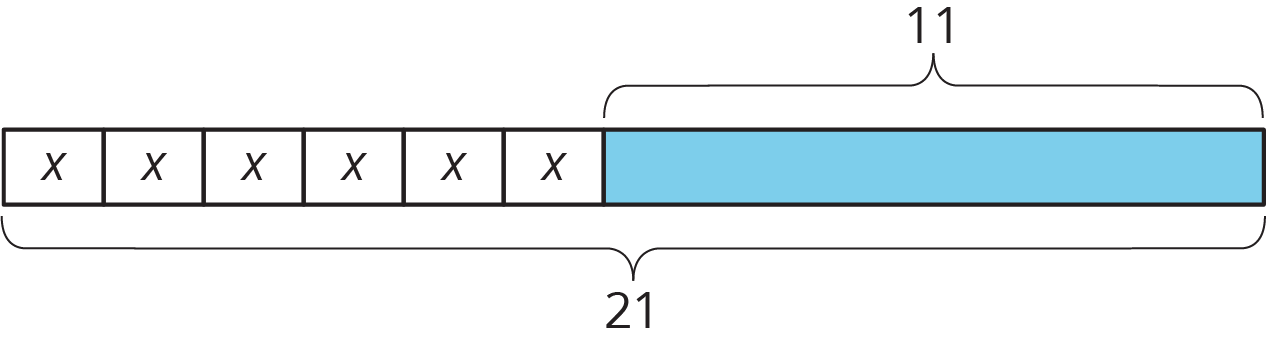
\(6x+11=21\)
Problema 5
- Ubica estos puntos en el plano de coordenadas:
\(A= (3, 2), B= (7.5, 2), C= (7.5, \text-2.5), D= (3, \text-2)\)

- ¿Cuál es la diferencia vertical entre \(D\) y \(A\)?
- Escribe una expresión que represente la distancia vertical entre \(B\) y \(C\).