Glosario
-
al cuadrado
Usamos la expresión al cuadrado para decir "elevado a la potencia de 2". Esta expresión viene del hecho de que un cuadrado con lados de longitud \(s\) tiene área \(s⋅s\), es decir \(s^2\).
-
al cubo
Usamos la expresión al cubo para decir "a la potencia de 3". Esta expresión viene del hecho de que un cubo con lados de longitud \(s\) tiene volumen \(s⋅s⋅s\), es decir \(s^3\).
-
altura (de un paralelogramo o un triángulo)
La altura es la distancia más pequeña de la base de la figura al lado opuesto (en un paralelogramo) o al vértice opuesto (en un triángulo).
Podemos dibujar la altura en distintos lugares. Independientemente de la posición, siempre será perpendicular al lado que se tomó como base.
-
área
El área de una región bidimensional es el número de cuadrados unitarios que la cubre sin que queden espacios vacíos ni haya superposiciones.
Por ejemplo, el área de la región A es 8 unidades cuadradas. El área de la región sombreada de B es \(\frac12\) unidad cuadrada.
-
área de superficie
El área de superficie de un poliedro es el número de cuadrados unitarios necesarias para recubrir todas las caras del poliedro sin que queden espacios vacíos ni haya superposiciones.
Por ejemplo, si las caras de un cubo tienen 9 cm2 de área cada una, entonces el área de superficie del cubo es \(6 \boldcdot 9\), es decir 54 cm2.
-
arista (o lado)
A los lados rectos de un polígono se les llama aristas o lados.
Por ejemplo, las aristas (o lados) de este polígono son los segmentos \(\overline{AB}\), \(\overline{BC}\), \(\overline{CD}\), \(\overline{DE}\) y \(\overline{EA}\).
-
base (de un paralelogramo o un triángulo)
Podemos elegir cualquier lado de un paralelogramo o un triángulo como su base. A menudo usamos la palabra base para referirnos a la longitud de ese lado.
-
base (de un prisma o pirámide)
La palabra base también se usa para referirse a una cara de un poliedro.
Un prisma tiene dos bases idénticas que son paralelas. Una pirámide tiene una sola base.
El nombre de un prisma o una pirámide viene de la forma de su base.
-
cara
Cada lado plano de un poliedro es llamado una cara. Por ejemplo, un cubo tiene 6 caras y todas son cuadrados.
-
centro
El centro de un conjunto de datos numéricos es un valor en el medio de la distribución. Este valor representa un valor típico para el conjunto de datos.
Por ejemplo, el centro de esta distribución de pesos de gatos se encuentra entre 4.5 y 5 kilogramos.
-
coeficiente
El coeficiente de una variable es el número que la multiplica.
Por ejemplo, en la expresión \(3x+5\), el coeficiente de la \(x\) es 3. En la expresión \(y+5\), el coeficiente de la \(y\) es 1, porque \(y=1 \boldcdot y\). En la expresión \(\frac{3x}{4}-2\) el coeficiente de la \(x\) es \(\frac34\), porque \(\frac{3x}{4}=\frac34 \boldcdot x\).
-
componer
Componer significa "juntar" o "unir". Usamos la palabra componer para describir el proceso de juntar o unir más de una figura para crear una nueva figura.
-
cuadrante
El plano de coordenadas está dividido en 4 regiones llamadas cuadrantes. Los cuadrantes se numeran usando números romanos y comenzando en la esquina superior derecha.
-
cuadrilátero
Un cuadrilátero es un polígono que tiene exactamente 4 lados. Los rectángulos son ejemplos de cuadriláteros. Un pentágono no es un cuadrilátero porque tiene 5 lados.
-
cuartil
Los cuartiles son los números que separan un conjunto de datos ordenado de menor a mayor en cuatro partes, cada una con igual cantidad de datos.
Por ejemplo, en este conjunto de datos el primer cuartil es 25. El segundo cuartil es lo mismo que la mediana, que es 33. El tercer cuartil es 40.
12 19 25 27 28 33 34 35 40 40 49 Q1 Q2 Q3 -
datos categóricos
En un conjunto de datos categóricos los valores de los datos son palabras en vez de números.
Por ejemplo, Han le pide a 5 amigos que digan su color favorito. Sus respuestas son: azul, azul, verde, azul, naranja.
-
datos numéricos
Un conjunto de datos numéricos es una colección de datos que son números.
Por ejemplo, Han hace una lista de las edades de las personas de su familia: 7, 10, 12, 36, 40, 67.
-
desarrollo plano
Un desarrollo plano es una figura bidimensional que puede doblarse para armar un poliedro. Este es un desarrollo plano de un cubo.
-
descomponer
Descomponer significa "separar". Usamos la palabra descomponer para describir el separar una figura para crear varias figuras nuevas.
-
desviación media absoluta (MAD)
La desviación media absoluta es una medida de la dispersión de un conjunto de datos. A veces la llamamos la MAD (por sus siglas en inglés). Por ejemplo, para el conjunto de datos 7, 9, 12, 13, 14, la MAD es 2.4. Esto nos dice que estos tiempos de viaje están, por lo general, a 2.4 minutos de diferencia de la media que es 11.
Para encontrar la MAD, sumamos las distancias de cada dato a la media y después dividimos entre la cantidad de datos. \(4+2+1+2+3=12\), y \(12 \div 5 = 2.4\).
-
diagrama de caja
Un diagrama de caja es una forma de representar un resumen de unos datos en una recta numérica. Los datos de separan en cuatro partes. Los lados de la caja representan el primer y tercer cuartil. La línea dentro de la caja representa la mediana. Las líneas por fuera de la caja la conectan con los valores mínimo y máximo.
Por ejemplo, este diagrama de caja muestra un conjunto de datos con 2 como valor mínimo y 15 como valor máximo. La mediana es 6, el primer cuartil es 5 y el tercer cuartil es 10.
-
diagrama de cinta
Un diagrama de cinta es un una colección de rectángulos que se unen para representar una relación entre cantidades.
Por ejemplo, este diagrama de cinta muestra una razón de 30 galones de pintura amarilla a 50 galones de pintura azul.
Si cada rectángulo se marcara con 5, en vez de 10, entonces la misma imagen podría representar la razón equivalente de 15 galones de pintura amarilla a 25 galones de pintura azul.
-
diagrama de puntos
Un diagrama de puntos es una forma de representar datos en una recta numérica. Cada vez que un valor aparece en el conjunto de datos, ponemos un nuevo punto encima de ese valor en la recta numérica.
Por ejemplo, en este diagrama de puntos hay tres puntos encima del 9. Esto significa que hay tres plantas distintas con altura 9 cm.
-
diagrama de recta numérica doble
En un diagrama de recta numérica doble se usan dos rectas paralelas para representar razones equivalentes. Las marcas se encuentran alineadas en ambas rectas de acuerdo a la equivalencia. Las marcas del 0 coinciden, pero las de otros números por lo general son diferentes.
3 cucharaditas de pintura roja corresponden a 5 cucharaditas de pintura amarilla. La razón es \(3:5\) (que es equivalente a \(6:10\), \(9:15\), etc.). Por eso 3 está alineado con 5, 6 está alineado con 10, 9 está alineado con 15, etc.
-
dispersión
La dispersión de un conjunto de datos numéricos nos dice qué tan separados están los valores.
Por ejemplo, estos dos diagramas de puntos muestran que las duraciones de viaje de los estudiantes de Sudáfrica están más dispersas que las de los estudiantes de Nueva Zelanda.
-
distribución
La distribución nos dice cuántas veces que aparece cada valor en un conjunto de datos. Por ejemplo, en el conjunto de datos "azul, azul, verde, azul, naranja", la distribución es 3 azules, 1 verde y 1 naranja.
Este diagrama de puntos muestra la distribución del conjunto de datos 6, 10, 7, 35, 7, 36, 32, 10, 7, 35.
-
división larga
La división larga es un proceso que nos permite encontrar la forma decimal del cociente de dos números. En este proceso se va encontrando dígito a dígito, de izquierda a derecha.
Por ejemplo, este es un ejemplo del uso de la división larga para encontrar \(57 \div 4\).
\(\displaystyle \require{enclose} \begin{array}{r} 14.25 \\[-3pt] 4 \enclose{longdiv}{57.00}\kern-.2ex \\[-3pt] \underline{-4\phantom {0}}\phantom{.00} \\[-3pt] 17\phantom {.00} \\[-3pt]\underline{-16}\phantom {.00}\\[-3pt]{10\phantom{.0}} \\[-3pt]\underline{-8}\phantom{.0}\\ \phantom{0}20 \\[-3pt] \underline{-20} \\[-3pt] \phantom{00}0 \end{array} \) -
exponente
En expresiones como \(5^3\) y \(8^2\), el 3 y el 2 se llaman exponentes. Estos nos indican cuántas veces multiplicar cada número por sí mismo. Por ejemplo, \(5^3\) = \(5 \boldcdot 5 \boldcdot 5\) y \(8^2 = 8 \boldcdot 8\).
-
expresiones equivalentes
Dos expresiones numéricas son equivalentes si tienen el mismo valor. Dos expresiones con variables son equivalentes si, al remplazar la variable por cualquier número, siempre dan el mismo valor.
Por ejemplo, \(2(7-3)+2\) es equivalente a \(\frac{35+5}{4}\), porque ambas expresiones valen 10. La expresión con variables \(3x+4x\) es equivalente a \(5x+2x\), porque sin importar qué valor le demos a \(x\), estas expresiones siempre valdrán lo mismo. Cuando \(x=3\), ambas expresiones valen 21. Cuando \(x=10\), ambas expresiones valen 70.
-
factor común
Un factor común de dos números es un número que divide a ambos exactamente (sin dejar residuo). Por ejemplo, 5 es un factor común de 15 y 20, porque \(15 \div 5 = 3\) y \(20 \div 5 = 4\). Ambos cocientes, 3 y 4, son números enteros. En otras palabras, un factor común de dos números enteros es un factor que estos números tienen en común
- Los factores de 15 son 1, 3, 5 y 15.
- Los factores de 20 son 1, 2, 4, 5, 10 y 20.
Así, un factor común de 15 y 20 es 5.
-
frecuencia
La frecuencia de un valor es el número de veces que aparece en el conjunto de datos.
Por ejemplo, había 20 perros en un parque. La tabla muestra la frecuencia de cada color de perro.
color frecuencia blanco 4 marrón 7 negro 3 multicolor 6 -
histograma
Un histograma es una forma de representar datos sobre una recta numérica. Los datos se agrupan en rangos de valores. La altura de la barra muestra el número de datos que se encuentran en ese rango de valores.
Por ejemplo, este histograma muestra que hubo 10 personas que recibieron 2 o 3 boletos. No podemos saber cuántas personas recibieron exactamente 2 boletos, o cuántas personas recibieron exactamente 3 boletos. Cada barra incluye el valor del extremo izquierdo pero no el valor del extremo derecho. (Hubo 12 personas que recibieron 4 o 5 boletos y 13 personas que recibieron 6 o 7 boletos.)
-
máximo factor común
El máximo factor común de dos números es el número entero más grande que divide a ambos números sin dejar residuo. A veces nos referimos a este número como GCF (por sus siglas en inglés) o MFC. Por ejemplo, 15 es el máximo factor común de 45 y 60.
- Los factores de 45 son 1, 3, 5, 9, 15 y 45.
- Los factores de 60 son 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 y 60.
-
media
La media es una medida de centro de un conjunto de datos. Podemos pensar en la media como un punto de equilibrio. Por ejemplo, para el conjunto de datos 7, 9, 12, 13, 14, la media es 11.
Para encontrar la media, sumamos todos los números en el conjunto de datos y después dividimos entre la cantidad de datos. \(7+9+12+13+14=55\) y \(55 \div 5 = 11\).
-
mediana
La mediana es una medida de centro de un conjunto de datos. Es el valor que queda en el medio cuando escribimos los datos en orden.
En el conjunto de datos 7, 9, 12, 13, 14, la mediana es 12.
En el conjunto de datos 3, 5, 6, 8, 11, 12, hay dos números en el medio. La mediana es 7, el promedio de estos dos números. \(6+8=14\) y \(14 \div 2=7\).
-
medida de centro
Una medida de centro es un valor que parece ser típico en una distribución de datos.
La media y la mediana son ambas medidas de centro.
-
metros por segundo (metros por cada segundo)
Metros por segundo es una unidad para medir la velocidad o rapidez. Nos indica cuánto recorre un objeto en un segundo (cuántos metros por cada segundo).
Por ejemplo, una persona que camina a 3 metros por segundo se está moviendo más rápido que otra que camina a 2 metros por segundo.
-
mínimo común múltiplo
El mínimo común múltiplo de dos números es el menor número que es un múltiplo de ambos. A veces nos referimos a esté como el LCM (por sus siglas en inglés) o el MCM. Por ejemplo, 30 es el mínimo común múltiplo de 6 y 10.
- Los múltiplos de 6 son 6, 12, 18, 24, 30, 36, 42, 48, 54, 60 . . .
- Los múltiplos de 10 son 10, 20, 30, 40, 50, 60, 70, 80 . . .
Los números 6 y 10 tienen varios múltiplos en común (30, 60, 90, . . .). El menor de ellos es 30.
-
misma tasa
Usamos las palabras misma tasa para describir situaciones que involucran razones equivalentes.
Por ejemplo, un lavabo se está llenando a una tasa de 2 galones por cada minuto. Si una bañera se está llenando a una tasa de 4 galones por cada 2 minutos, entonces el lavabo y la bañera se están llenando a la misma tasa.
-
múltiplo común
Un múltiplo común de dos números enteros es un número que se puede obtener al multiplicar cada uno de los números por algún número entero (que no tiene que ser el mismo). Por ejemplo, 30 es un múltiplo común de 3 y 5 porque \(3 \cdot 10 = 30\) y \(5 \cdot 6 = 30\). Ambos factores, 10 y 6, son números enteros.
- Los múltiplos de 3 son 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33 . . .
- Los múltiplos de 5 son 5, 10, 15, 20, 25, 30, 35, 40 . . .
Así los múltiplos comunes de 3 y 5 son 15, 30, 45, 60 . . .
-
número negativo
Un número negativo es un número que es menor que cero. En la recta numérica horizontal, los números negativos usualmente se muestran a la izquierda del 0.
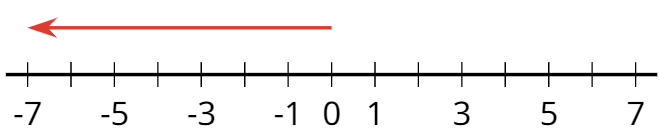
-
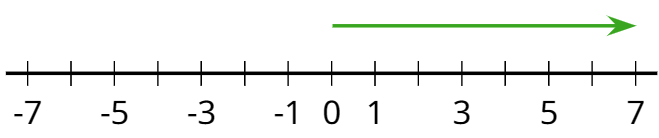
número positivo
Un número positivo es un número que es mayor que cero. En la recta numérica horizontal, los números positivos usualmente se muestran a la derecha del 0.
-
número racional
Un número racional es una fracción o el opuesto de una fracción.
Por ejemplo, 8 y -8 son números racionales porque se pueden escribir como \(\frac81\) y \(\text-\frac81\).
Los números 0.75 y -0.75 también son números racionales porque se pueden escribir como \(\frac{75}{100}\) y \(\text-\frac{75}{100}\).
-
opuestos
Dos números son opuestos si al ubicarlos sobre la recta numérica están a lados opuestos del 0 pero a la misma distancia del 0.
Por ejemplo, 4 es el opuesto de -4 y -4 es el opuesto de 4. Ambos están a la misma distancia de 0. Uno de ellos es negativo y el otro es positivo.
-
paralelogramo
Un paralelogramo es un tipo de cuadrilátero que tiene dos parejas de lados paralelos.
Estos son dos paralelogramos.
-
pirámide
Una pirámide es un tipo de poliedro que tiene una base. Todas las demás caras son triángulos que se encuentran en un solo vértice.
Estos son unos dibujos de pirámides.
-
plano de coordenadas
El plano de coordenadas es un sistema para especificar la ubicación de puntos. Por ejemplo, el punto \(R\) está ubicado en \((3, 2)\) en el plano de coordenadas, porque está tres unidades a la derecha y dos unidades arriba del origen.
-
poliedro
A poliedro es una figura tridimensional, cerrada, con caras planas.
Estos son unos dibujos de poliedros.
-
polígono
Un polígono es una figura bidimensional, cerrada, compuesta por segmentos de recta que no se cruzan entre sí.
Por ejemplo, la figura \(ABCDE\) es un polígono.
-
porcentaje
Un porcentaje es una tasa por cada 100.
Por ejemplo, una pecera puede contener 36 litros. En este momento solo hay 27 litros en la pecera. El porcentaje de la pecera que está lleno es 75%.
-
por ciento
La frase por ciento significa "por cada 100". El símbolo para por ciento es %.
Por ejemplo, una moneda de un cuarto de dólar tiene un valor de 25 centavos, y un dólar tiene un valor de 100 centavos. Podemos decir que una moneda de un cuarto de dólar vale 25% de un dólar.
-
por (o por cada)
La palabra por significa "por cada" en contextos en los que se relacionan magnitudes o unidades de medida. Por ejemplo, si el precio es \$5 por boleto, esto significa que uno pagará \$5 por cada boleto. Comprar 4 boletos costaría \$20, porque \(4 \boldcdot 5 = 20\).
-
precio unitario
El precio unitario es el costo de un artículo o de una unidad de medida. Por ejemplo, si 10 pies de cadena cuestan \$150, entonces el precio unitario es \(150 \div 10\), es decir \$15 por cada pie de cadena.
-
pregunta estadística
Una pregunta estadística es una pregunta que se puede responder recolectando datos que tengan variabilidad. Estos son algunos ejemplos de preguntas estadísticas:
- ¿Cuántos minutos dedican los estudiantes de grado 6 a hacer tareas cada semana?
- ¿Cuál es la hora típica en la cual se acuesta a dormir un estudiante de grado 7?
- ¿Cuántas mascotas tiene un estudiante de grado 8?
-
prisma
Un prisma es un tipo de poliedro que tiene dos bases iguales. Las bases están conectadas por rectángulos o paralelogramos.
Estos son dibujos de prismas.
-
promedio
El promedio es otro nombre que se usa para la media de un conjunto de datos.
El promedio del conjunto de datos 3, 5, 6, 8, 11, 12, es 7.5.
\(3+5+6+8+11+12=45\)
\(45 \div 6 = 7.5\)
-
rango
El rango es la distancia entre el valor más pequeño y el valor más grande en un conjunto de datos. Por ejemplo, en el conjunto de datos 3, 5, 6, 8, 11, 12, el rango es 9 porque \(12-3=9\).
-
rango intercuartil (IQR)
El rango intercuartil es una forma de medir qué tan dispersos están los datos. A menudo nos referimos a este como el IQR (por sus siglas en inglés). Para encontrar el rango intercuartil restamos el valor del primer cuartil del valor del tercer cuartil.
Por ejemplo, el IQR de este conjunto de datos es 20 porque \(50-30=20\).
22 29 30 31 32 43 44 45 50 50 59 Q1 Q2 Q3 -
rapidez
La rapidez es una forma de describir que tan rápido se mueve algo. La rapidez nos dice cuánto recorre un objeto en una cierta cantidad de tiempo.
Por ejemplo, Tyler camina a una rapidez de 4 millas por cada hora (o 4 millas por hora). Priya camina a una rapidez de 5 millas por cada hora. Priya camina más rápido que Tyler, porque recorre una distancia mayor en la misma cantidad de tiempo.
-
razón
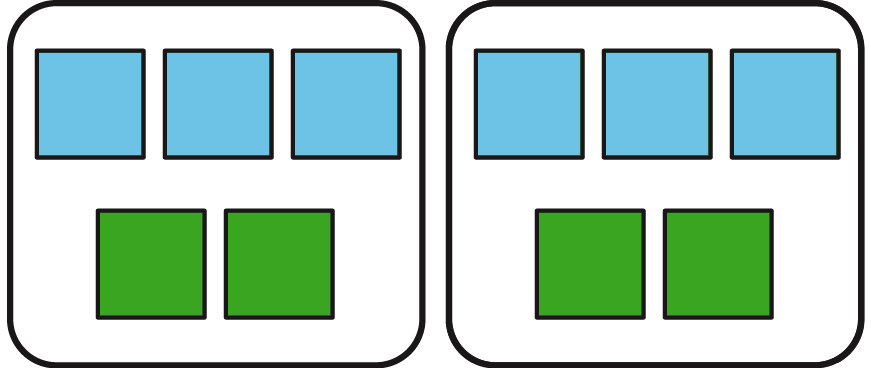
Una razón es una asociación entre dos o más cantidades.
Por ejemplo, la razón \(3:2\) podría describir una receta que usa 3 tazas de harina por cada 2 huevos, o un bote que recorre 3 metros cada 2 segundos. Una forma de representar la razón \(3:2\) es con un diagrama que tiene 3 cuadrados azules por cada 2 cuadrados verdes.
-
razones equivalentes
Dos razones son equivalentes si puedes multiplicar cada uno de los números de la primera razón por el mismo factor y obtener los números de la segunda razón. Por ejemplo, \(8:6\) es equivalente a \(4:3\) porque \(8\boldcdot\frac12 = 4\) y \(6\boldcdot\frac12 = 3\).
Una receta de limonada indica que se deben usar 8 tazas de agua y 6 limones. Si usamos 4 tazas de agua y 3 limones, vamos a producir la mitad de la cantidad de limonada. Ambas recetas saben igual, porque \(8:6\) y \(4:3\) son razones equivalentes.
tazas de agua número de limones 8 6 4 3 -
recíproco
Al dividir 1 entre un número, se obtiene el recíproco de ese número. Por ejemplo, el recíproco de 12 es \(\frac{1}{12}\) y el recíproco de \(\frac25\) es \(\frac52\).
-
región
Una región es un espacio delimitado por una figura. Algunos ejemplos de regiones bidimensionales son lo que hay dentro de un círculo, lo que hay fuera de un polígono, o lo que hay a la derecha del eje \(y\). Algunos ejemplos de regiones tridimensionales son lo que hay dentro de un cubo o fuera de una esfera.
-
ritmo
El ritmo es una forma de describir que tan rápido se mueve algo. El ritmo nos dice cuánto tiempo le toma a un objeto recorrer una cierta distancia.
Por ejemplo, Diego camina a un ritmo de 10 minutos por cada milla. Elena camina a un ritmo de 11 minutos por cada milla. Elena camina más despacio que Diego, porque le toma más tiempo recorrer la misma distancia.
-
signo
El signo de cualquier número distinto de cero es positivo o negativo.
Por ejemplo, el signo de 6 es positivo. El signo de -6 es negativo. El cero no tiene signo, porque no es positivo ni negativo.
-
solución de una desigualdad
La solución de una desigualdad es un número que al reemplazar a la variable hace que la desigualdad sea verdadera.
Por ejemplo, 5 es una solución de la desigualdad \(c<10\), porque \(5<10\) es cierto. Otras soluciones de esta desigualdad son 9.9, 0 y -4.
-
solución de una ecuación
Una solución de una ecuación es un número que al reemplazar a la variable hace que la ecuación sea verdadera.
Por ejemplo, 7 es la solución de la ecuación \(m+1=8\), porque \(7+1=8\) es cierto. En cambio, 9 no es solución de \(m+1=8\), porque \(9+1\ne8\).
-
tabla
Una tabla organiza información en filas horizontales y columnas verticales. Por lo general, la primera fila o columna nos indica lo que representan los números. Por ejemplo, esta tabla muestra las longitudes de las colas de tres mascotas. La tabla tiene cuatro filas y dos columnas.
mascota longitud de la cola (pulgadas) perro 22 gato 12 ratón 2 -
tasa unitaria
Una tasa unitaria es una tasa por cada 1.
Por ejemplo, 12 personas comparten 2 tartas de manera equitativa. Una tasa unitaria es 6 personas por cada tarta, porque \(12 \div 2 = 6\). La otra tasa unitaria es \(\frac16\) de tarta por cada persona, porque \(2 \div 12 = \frac16\).
-
término
Un término es una parte de una expresión. Puede ser un solo número, una variable, o la multiplicación de un número con una variable. Por ejemplo, la expresión \(5x + 18\)tiene dos términos: el primer término es \(5x\) y el segundo término es 18.
-
valor absoluto
El valor absoluto de un número es su distancia al 0 en la recta numérica.
El valor absoluto de -7 es 7, porque -7 está a 7 unidades del 0. El valor absoluto de 5 es 5, porque 5 está a 5 unidades del 0.
-
variabilidad
La variabilidad significa que los valores de los datos no son todos iguales.
Por ejemplo, el conjunto de datos B tiene una mayor variabilidad que el conjunto de datos A. El conjunto de datos B tiene muchos valores distintos, mientras que el conjunto de datos A tiene más datos con los mismos valores.
-
variable
Una variable es una letra que representa un número. Puedes elegir distintos números como valores de la variable.
Por ejemplo, en la expresión \(10-x\), la variable es \(x\). Si el valor de \(x\) es 3, entonces \(10-x=7\), porque \(10-3=7\). Si el valor de \(x\) es 6, entonces \(10-x=4\), porque \(10-6=4\).
-
variable dependiente
La variable dependiente es el resultado de un cálculo. Por ejemplo, un barco viaja a una rapidez constante de 25 millas por hora. La ecuación \(d=25t\) describe la relación entre la distancia recorrida por el bote y el tiempo transcurrido. La variable dependiente es la distancia recorrida porque \(d\) es el resultado de multiplicar 25 por \(t\).
-
variable independiente
La variable independiente se usa para calcular el valor de otra variable. Por ejemplo, un barco viaja a una rapidez constante de 25 millas por hora. La ecuación \(d=25t\) describe la relación entre la distancia recorrida por el bote y el tiempo transcurrido. La variable independiente es el tiempo transcurrido porque \(t\) es multiplicado por 25 para obtener \(d\).
-
vértice
Un vértice es un punto en donde dos o más aristas se encuentran. Los vértices de este polígono están etiquetados con las letras \(A\), \(B\), \(C\), \(D\) y \(E\).
-
vértice opuesto
Para cada lado de un triángulo hay un vértice que no está sobre ese lado. A este lo llamamos el vértice opuesto (opuesto a ese lado).
Por ejemplo, el punto \(A\) es el vértice opuesto al lado \(BC\).
-
volumen
El volumen de una región tridimensional es el número de unidades cúbicas que la llenan, sin espacios ni superposiciones.
Por ejemplo, el volumen de este prisma rectangular es 60 unidades3, pues está compuesto por 3 capas, cada una de 20 unidades3.